Куб из проволоки – Как сделать кубик из проволоки

Как сделать кубик из проволоки

Сделаем из проволоки кубик (куб).

Продолжаем серию уроков «Поделки из проволоки». В прошлый раз  изготовляли  несложные  геометрические  фигуры – это задание для 5-7 леток. Но вот пришла группа постарше – первый-второй класс. За этот год руки и глазомер у них здорово развились, и им можно давать весьма сложные задания.

– Кубик из проволоки сделаете?

О! Вот ценю таких людей – с  энтузиазмом взялись экспериментировать, хотя видно, что с проволокой тоже  не знакомы… Я раздала длинные-длинные отрезки проволоки и посоветовала концы загнуть петлей, чтобы не поцарапаться. Кстати, ребята сделали свои кубы из проволоки без предварительного плана, просто подбором. Не сказать, что кубики вышли идеальные, но я возгордилась – верить надо в детей – когда хотят, могут творить чудеса.

Куб из проволоки – изделие ученика

Причём некоторые даже сумели точно уложиться в предложенную длину отрезка использовали без остатка:

А вам я расскажу немножко теории.

Этапы изготовления кубика из  проволоки.

Итак, рисуем куб и считаем стороны – 12 штук.

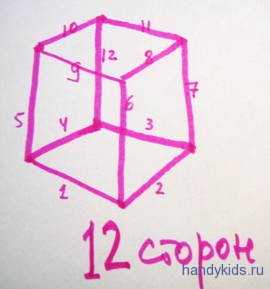
Но мы понимаем, что недостаточно просто взять проволоку и перегнуть пополам, потом каждую половину пополам и потом на три поделить – и типа это стороны куба. Это сложно, неточно и – самое главное – из одного куска проволоки  просто так куб не получится: или придётся некоторые стороны сделать двойные, или диагонали потребуются. Вобщем, с делением на 12 частей  утопия не осуществима.

Присмотримся к нашей схеме – вот малиновым я рисую последовательность сторон(начало-зелёная точка):

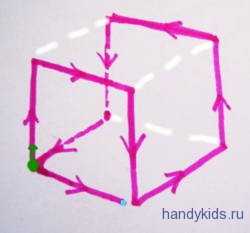
Дойдя до угла с синей точкой мы вынуждены признать – три стороны не пройдены и недостижимы.

Как выход вот такие два варианта: из двух  кусков проволоки и из одного, но с повторами и диагоналями.

Как изготовляла я сама? А наобум. Взяла проволоку без изоляции в надежде, что углы получатся чётче, чем с изоляцией – (она скругляет).

Да вот, сначала придётся распрямлять

Итак, распрямила проволоку – с силой продавливая, протянула поперёк металлического края стола.

И просто начала сгибать стороны.

Первые шаги даются сравнительно легко, но сразу обнаруживается сложность: свободный длинный конец проволоки мотается и чуть зазевайся, норовит хлестнуть по рукам и лицу.

Но вот пора закреплять углы. Как? Петлями обматывать – как ещё?

Оформление углов куба

Тут проволока превзошла себя, извиваясь и запутываясь. Но я оказалась настойчивее – вот моя конструкция:

Как сделать кубик из проволоки вам рассказала Марина Новикова.

Метки: поделки из подручных материалов, поделки из проволоки

Читайте также:

Google+

Марина Новикова

handykids.ru

Куб из проволоки своими руками. Кубик из проволоки

Сделаем из проволоки кубик (куб).

Продолжаем серию уроков «Поделки из проволоки». В прошлый раз – это задание для 5-7 леток. Но вот пришла группа постарше – первый-второй класс. За этот год руки и глазомер у них здорово развились, и им можно давать весьма сложные задания.

Кубик из проволоки сделаете?

О! Вот ценю таких людей – с энтузиазмом взялись экспериментировать, хотя видно, что с проволокой тоже не знакомы… Я раздала длинные-длинные отрезки проволоки и посоветовала концы загнуть петлей, чтобы не поцарапаться. Кстати, ребята сделали свои кубы из проволоки без предварительного плана, просто подбором. Не сказать, что кубики вышли идеальные, но я возгордилась – верить надо в детей – когда хотят, могут творить чудеса.

Куб из проволоки – изделие ученика

Причём некоторые даже сумели точно уложиться в предложенную длину отрезка использовали без остатка:

А вам я расскажу немножко теории.

Этапы изготовления кубика из проволоки.

Итак, рисуем куб и считаем стороны – 12 штук.

Но мы понимаем, что недостаточно просто взять проволоку и перегнуть пополам, потом каждую половину пополам и потом на три поделить – и типа это стороны куба. Это сложно, неточно и – самое главное – из одного куска проволоки просто так куб не получится: или придётся некоторые стороны сделать двойные, или диагонали потребуются. Вобщем, с делением на 12 частей утопия не осуществима.

Присмотримся к нашей схеме – вот малиновым я рисую последовательность сторон(начало-зелёная точка):

Дойдя до угла с синей точкой мы вынуждены признать – три стороны не пройдены и недостижимы.

Как выход вот такие два варианта: из двух кусков проволоки и из одного, но с повторами и диагоналями.

Как изготовляла я сама? А наобум. Взяла проволоку без изоляции в надежде, что углы получатся чётче, чем с изоляцией – (она скругляет).

Да вот, сначала придётся распрямлять

Итак, распрямила проволоку – с силой продавливая, протянула поперёк металлического края стола.

И просто начала сгибать стороны.

1. Сколько кубиков?

Куб, окрашенный, например, в зеленый цвет, распилен на маленькие кубики, как показано на рисунке. Скажите (на размышление дается 1 минута):

• Сколько получится кубиков совсем неокрашенных?
• У скольких, кубиков окрашенной будет 1 грань?
• У скольких кубиков будут окрашены 2 грани?
• У скольких кубиков окрашенными будут 3 грани?

2. Куб из проволоки.

Ребра куба сделаны из проволоки, причем ни одно из них не получилось двойным. Каково наименьшее число отрезков проволоки, необходимое для решения задачи? Предположим теперь, что из проволоки сделаны не только ребра куба, но и его диагонали. Каким в этом случае окажется наименьшее число необходимых отрезков проволоки?

1. Сколько кубиков? Неокрашенных — 1, с одной окрашенной гранью — 6, с двумя — 12, с тремя — 8.

2. Куб из проволоки. В первом случае 4 отрезка: 1267; 2348; 3785; 6514 (возможен и другой путь). Во втором случае понадобится лишь один отрезок, который следует сгибать по «маршруту»: 1—5—6—7—8—5—3—7—1— 2—6—4—3—2—8—4—1.

«Твое свободное время», В.Н.Болховитинов, Б.И.Колтовой

Около небольшого белого домика на опушке леса две недели назад в 23.30 был найден труп некоего Л. Клемпнера. Следствие зашло в тупик, и, как всегда в таких случаях, на помощь был вызван инспектор Варнике. — Это произошло следующим образом,— начал рассказывать свидетель М. во время осмотра инспектором места происшествия.— Я ехал на велосипеде вдоль опушки…

С наступлением затяжных осенних дождей семейство Виммер покинуло дачу и вернулось в свою городскую квартиру. Еще до переезда Виммер договорился с соседом по даче неким З., чтобы тот присматривал за его хозяйством. Через несколько дней после Нового года З. позвонил Виммеру и взволнованным голосом сообщил, что Дача ограблена. Виммер тотчас же обратился в полицию, и…

— Вот здесь на опушке все и произошло, господин инспектор. Какой-то парень бросил мне в лицо молотый перец и выхватил из рук портфель, где находились деньги в сумме тысяча восемьсот пятьдесят семь марок. Я закричал, но вокруг никого не было. От страшного жжения в глазах я ничего не видел. К счастью, я знаю эту местность…

В одной из вилл на краю города 3. поселился некий Альфредо ди Мейро. Благодаря приятной наружности и аристократическим манерам ему удалось добиться расположения самых влиятельных людей города. Пользуясь необычайной популярностью в городе, дон Альфредо занимал деньги направо и налево. Когда же сумма его долгов приняла внушительные размеры, виллу Альфредо ди Мейро посетил инспектор Варнике. Хозяин…

— Я должен тщательно обыскать вашу квартиру, так как ваш сосед утверждает, что вчера, в новогоднюю ночь, в то время как он вместе с вашей семьей распевал веселые песенки под вашей елкой, сверкающей разноцветными лампочками, вы проникли в его квартиру и похитили у него ряд ценных вещей,— сказал инспектор Варнике, обращаясь к господину Майеру. —…

— Да отстаньте же вы от меня наконец! Я очень спешу. — Если вы сейчас же не остановитесь, я вынужден буду прибегнуть к крайним мерам,— сказал инспектор Варнике, как никогда кстати оказавшийся на месте происшествия.— Ведь это вы сейчас взяли в магазине перчатки и ушли, не заплатив за них! — Это неправда! Я действительно только…

Во время пребывания по делам службы в Калифорнии инспектору Варнике представился случай продемонстрировать местной полиции свои незаурядные способности. Однажды он был срочно вызван на аэродром, расположенный недалеко от Лос-Анджелеса. Из случайно услышанного телефонного разговора полиции стало известно, что рейс самолета, который отправляется на Аляску, закончится катастрофой. Один из пассажиров, намереваясь совершить самоубийство, берет с собой…

Вчера я вернулся домой со службы несколько раньше, чем обычно. Только я присел за стол, собираясь поужинать, как вдруг в комнате жены что-то упало. Я бросился туда и увидел лежащую на полу старинную вазу, которой моя жена очень дорожит. Ваза была разбита. В этот же момент из комнаты выбежал какой-то человек. Я кинулся за ним….

Из тюрьмы сбежал опасный преступник. Долгое время ему удавалось скрываться, но в конце концов инспектор Варнике напал на его след. В одной деревне ему и его спутнику сказали, что действительно какой-то неизвес

www.kalinark.ru

Как из проволоки сделать куб. Кубик из проволоки

Задумывались ли вы о том, как сделать куб из бумаги и зачем это нужно? Допустим, как сделать кубик из картона своими силами, мы вам расскажем и даже покажем. А какими полезными функциями вы наделите кубик оригами? Подскажем: вспомните свои детские кубики с буквами, из которых вы учились складывать первые слова, еще не умея писать. А если бумажный кубик оклеить картинками из старых детских книжек, получится не менее интересный, чем в нашем далеком детстве, пазл-конструктор.

Вариантов игрового применения куба из цветной бумаги не счесть. И при этом не придется переживать, что дети поранят друг друга, кидая такую игрушку. Наши-то деревянные были потяжелее. Мы уже готовы показать, как сделать кубик из бумаги своими руками прямо сейчас. Готовы приступать?

Простой бумажный кубик

Объемный шестигранный куб 3Д складывают из квадратного листка бумаги без клея. И даже ножницы здесь не потребуются. Разве что отрезать лишний «хвостик» от листа А4, чтобы получить заготовку-квадрат. Зато пригодится навык надувания воздушных шариков, ведь мы сейчас научим вас тому, как сделать надувной кубик. Заинтригованы? Тогда начнем:

• Схема 1 — ваш наглядный ориентир. К нему следует прибегать каждый раз, когда алгоритм складывания кажется сложным. Возьмите бумажный квадрат и сложите его по диагоналям, затем пополам — все это просто разметка;
• Ориентируясь на диагонали-сгибы, сформируйте треугольник, подгибая внутрь боковые плоскости заготовки (см. схему). 4 гуляющих угла у основания треугольника нужно подогнуть к вершине по 2 с каждой стороны заготовки;
• Боковые противоположные уголки подогните к центру — у вас здесь есть вертикальная ось-ориентир. Повторите действие с другой стороны. Гуляющие уголки одного из конических выступов (на втором углы «закрыты») дважды подгибают, чтобы их можно было аккуратно заправить в срединные уголки-кармашки;
• Аналогично заправьте дважды сложенные уголки в кармашки с обратной стороны заготовки. Модель куба готова, осталось дать ей объем. Найдите открытый уголок и через него надуйте макет.

Куб из модулей: сборный кубик 6 цветов

Как сделать кубик из картона своими силами мы уже рассмотрели выше, а для этого модульного куба будет достаточно разноцветной бумаги 6-ти расцветок (или 3-х повторяющихся). Он и без картона получится достаточно плотным за счет алгоритма складывания модулей (каждого в отдельности и всех воедино). Давайте начнем разбираться поэтапно. Сразу предупредим, что весь процесс будет разделен на 7 шагов — складывание модулей и сборка куба (можно на клей — будет прочнее). Какое-то время будет потрачено, но результат вас однозначно порадует: кубики получатся яркими, разноцветными, не нуждающимися в дополнительных украшениях или росписи.

• Возьмите квадратный листок бумаги и сложите его так, чтобы получилось видимое разделение на 4 одинаковых прямоугольных плоскости (см. рис. 2). Загните малые уголки по диагональным углам стартового квадрата;
• Заверните «створки» листа подобно закрытию оконных ставней. Используя ориентиры-уголки (подогнутые ранее), загните внутрь незадействованные прежде углы, потом заправите их внутрь с обеих сторон. Получится параллелограмм;
• Переверните конструкцию вниз лицом, отогните уголки к себе так, чтобы получился маленький квадрат с треугольными ушками-отгибами. Сделайте еще 5 шт. таких модулей.

Соединяйте блоки в куб, вводя уголки модулей в срединные плоскости-кармашки соседних блоков. Проявите смекалку, в крайнем случае поможет схема. Как сделать оригами кубик из ярких модулей, вы освоили на практике. Попробуйте склеить куб из блоков на этапе сборки, чтобы он был еще прочнее и не рассыпался на модули в игре. Можно, конечно, взять стандартную развертку куба, просто распечатать ее и склеить — готовые шаблоны всегда под рукой. А если типовая выкройка вас не устраивает и в игру нужен оригинальный счетный кубик, вы на раз-два сможете его сложить сами. Чего проще, когда знаешь, как сделать из бумаги еще и не такие премудрости. Возможно, вас заинтересуют схемы складывания

1. Сколько кубиков?

Куб, окрашенный, например, в зеленый цвет, распилен на маленькие кубики, как показано на рисунке. Скажите (на размышление дается 1 минута):

• Сколько получится кубиков совсем неокрашенных?
• У скольких, кубиков окрашенной будет 1 грань?
• У скольких кубиков будут окрашены 2 грани?
• У скольких кубиков окрашенными будут 3 грани?

2. Куб из проволоки.

Ребра куба сделаны из проволоки, причем ни одно из них не получилось двойным. Каково наименьшее число отрезков проволоки, необходимое для решения задачи? Предположим теперь, что из проволоки сделаны не только ребра куба, но и его диагонали. Каким в этом случае окажется наименьшее число необходимых отрезков проволоки?

1. Сколько кубиков? Неокрашенных — 1, с одной окрашенной гранью — 6, с двумя — 12, с тремя — 8.

2. Куб из проволоки. В первом случае 4 отрезка: 1267; 2348; 3785; 6514 (возможен и другой путь). Во втором случае понадобится лишь один отрезок, который следует сгибать по «маршруту»: 1—5—6—7—8—5—3—7—1— 2—6—4—3—2—8—4—1.

«Твое свободное время», В.Н.Болховитинов, Б.И.Колтовой

Около небольшого белого домика на опушке леса две недели назад в 23.30 был найден труп некоего Л. Клемпнера. Следствие зашло в тупик, и, как всегда в таких случаях, на помощь был вызван инспектор Варнике. — Это произошло следующим образом,— начал рассказывать свидетель М. во время осмотра инспектором места происшествия.— Я ехал на велосипеде вдоль опушки…

С наступлением затяжных осенних дождей семейство Виммер покинуло дачу и вернулось в свою городскую квартиру. Еще до переезда Виммер договорился с соседом по даче неким З., чтобы тот присматривал за его хозяйством. Через несколько дней после Нового года З. позвонил Виммеру и взволнованным голосом сообщил, что Дача ограблена. Виммер тотчас же обратился в полицию, и…

— Вот здесь на опушке все и произошло, господин инспектор. Какой-то парень бросил мне в лицо молотый перец и выхватил из рук портфель, где находились деньги в сумме тысяча восемьсот пятьдесят семь марок. Я закричал, но вокруг никого не было. От страшного жжения в глазах я ничего не видел. К счастью, я знаю эту местность…

В

www.kalinark.ru

Статья про Лайт-куб: “Делаем Лайт-куб своими руками”

? LiveJournal

• Main
• Ratings
• Interesting
• Disable ads

Login

• Login
• CREATE BLOG Join
• English (en)
  • English (en)
  • Русский (ru)
  • Українська (uk)
  • Français (fr)
  • Português (pt)
  • español (es)
  • Deutsch (de)
  • Italiano (it)
  • Беларуская (be)

vicnaum.livejournal.com

Задача про электрическое сопротивление куба – решение

Электрическое сопротивление куба

Дан каркас в виде куба, изготовленный из металлической проволоки. Электрическое сопротивление каждого ребра куба равно одному Ому. Чему равно сопротивление куба при прохождении электрического тока от одной вершины к другое, если он подключен к источнику постоянного тока как это показано на рисунке?

Решение задачи про электрическое сопротивление куба

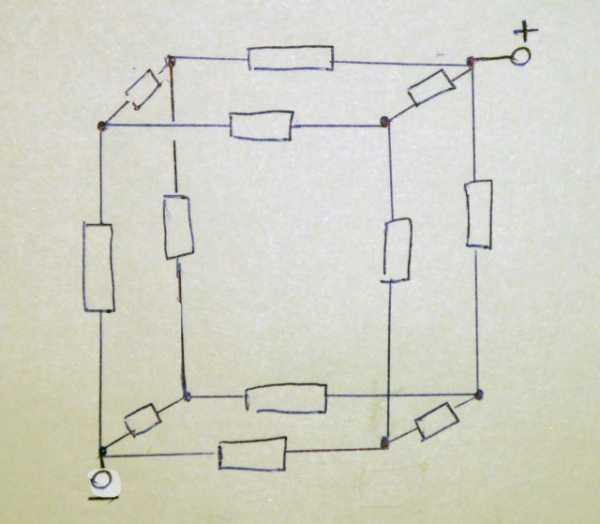	Рисуем куб резистров.
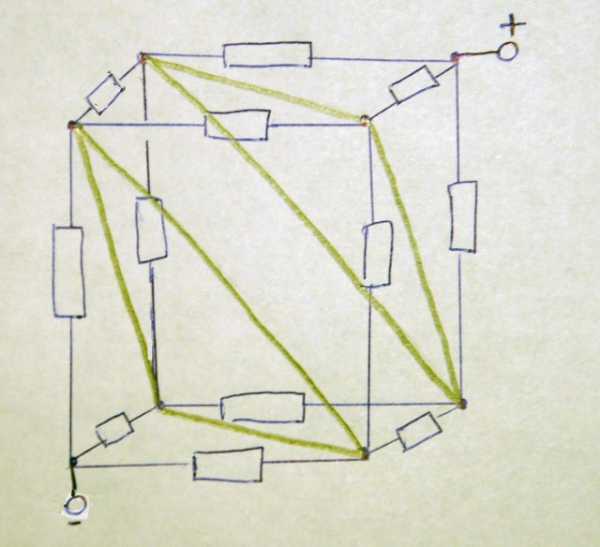	Соединяем дополнительными проводниками точки с равными напряжениями, ток через них течь не будет.
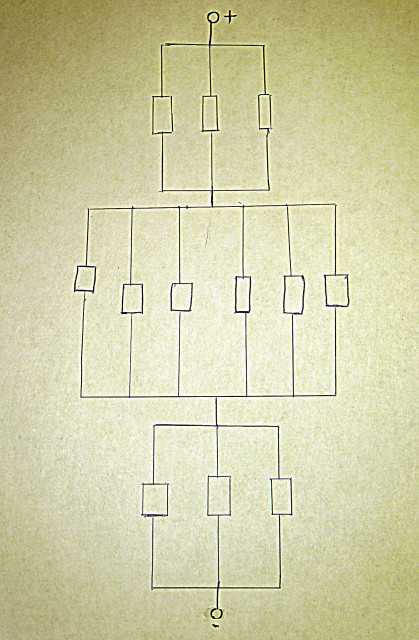	Упрощаем схему

Считаем сопротивление схемы по формулам для параллельного и последовательного подключения сопротивлений, получаем ответ – электрическое сопротивление куба равно 5/6 Ом.

Интересные факты про задачу про сопротивление куба резисторов

1. Решение задачки про сопротивление куба в общем виде можно прочитать на сайте журнала Квант или посмотреть здесь: “В конце сороковых годов в математических кружках Москвы появилась задача об электрическом сопротивлении проволочного куба. Кто ее придумал или нашел в старых учебниках мы не знаем. Задача была очень популярной, и о ней быстро узнали все. Очень скоро ее стали задавать на экзаменах и она стала почти тривиальной…” –  Ф.Недемейер, Я.Смородинский “Сопротивление ребер многомерного куба”.

Благодаря тому, что решение задачи про сопротивление куба неоднократно приводилось в сборниках задач, учебниках и т.п., она обычно не вызывает таких споров, как, например, задачка про самолет.

2. Задача может попасться на ЕГЭ. Это тоже является интересным фактом:)

3. Задачу про “сопротивление в кубе” можно решить более сложными способами, например, с помощью правил Кирхгофа. Вот одно из таких решений:

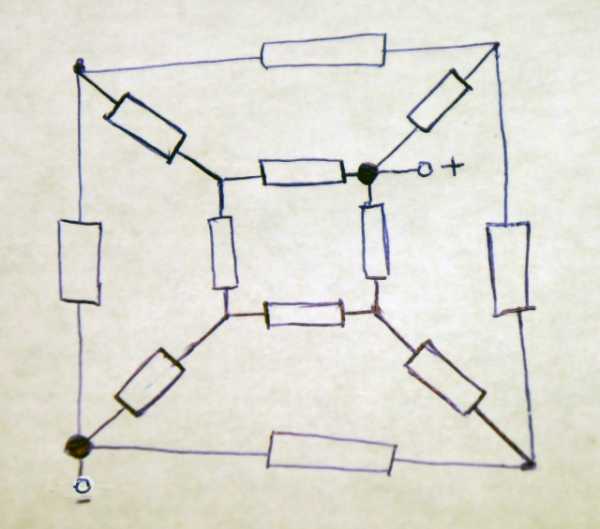
Изображаем куб резистров на плоскости в виде обычной электрической схемы.

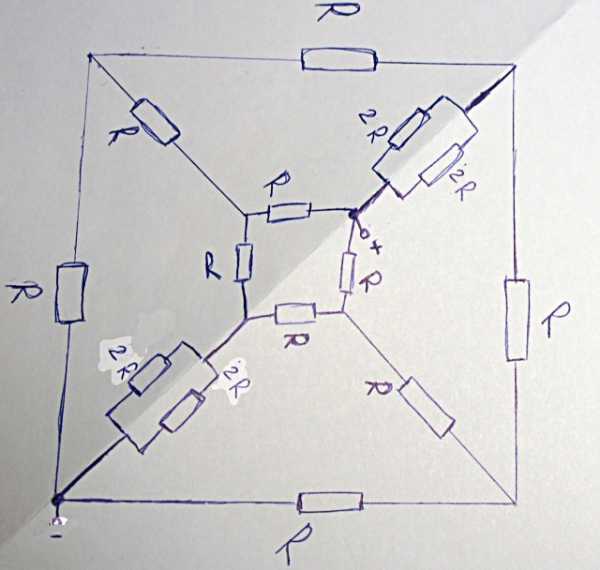
Обозначим все сопротивления ребер R. Заменяем 2 сопротивления R на эквивалентное им параллельное подключение сопротивлений по 2R каждое – как это показано выше на рисунке.

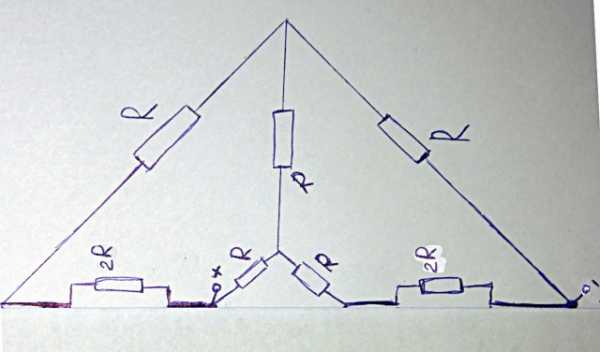
Мысленно сгибаем лист с изображенной на нем схемой пополам – вдоль оси симметрии. Получаем схему для “половины куба”, изображенную на рисунке выше. Обозначим ее сопротивление за Rх

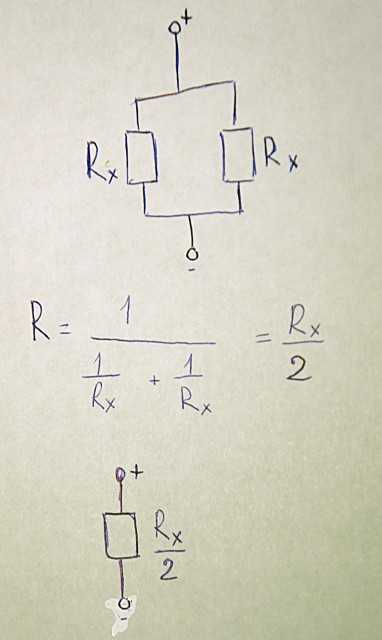
Рассуждаем следующим образом: по правой и левой половинам текут одинаковые токи, т.к. они абсолютно симметричны. Значит можно условно изобразить схему для сопротивления куба так как показано на рисунке выше: как два параллельных сопротивления, каждое из которых эквивалентно половине схемы. Общее сопротивление куба будет, таким образом, равно одной второй от сопротивления схемы Rх, изображенной ранее (см. схему для “половины” куба)

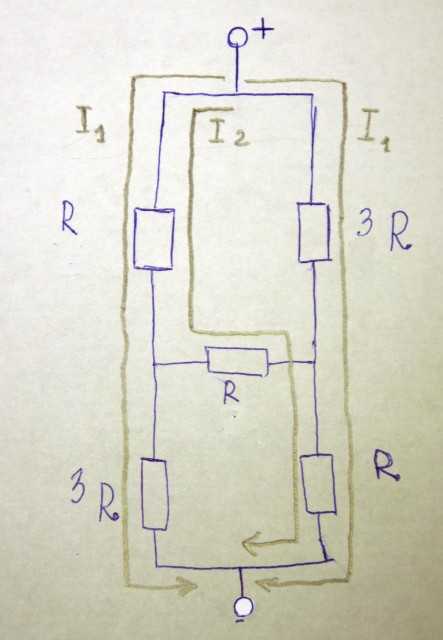
Преобразуем схему “для половины куба” в вид как показано на рисунке выше и найдем ее сопротивление Rх.

Обратим внимание, что токи, текущие через оба сопротивления 3R, равны в силу симметрии. Обозначим их за I1, а ток, текущий “посредине” – за I2.

Подсчитаем общее напряжение U двумя разными способами:
U=R(I1+I2)+3RI1=2R(I1+I2)+RI2

Отсюда следует, что ток I1=I2=I

Напряжение U можно выразить в виде уравнения через Rх:
U=Rх(I2 +2I1)=3IRх

Соотношение U/I найдем из любого другого уравнения, написанного выше.

Получим ответ Rх=5R/3, а значит сопротивление всего куба будет равно 5R/6.

————————————-
Такое решение задачи про сопротивление куба резистроров чем-то похоже на приведенное в самом начале. Разница лишь в том, что мы ищем на схеме не равные напряжения, а равные токи. Второй вариант решения получается громоздким и сводится к решению другой, достаточно сложной задачи.

anton7777777.livejournal.com